t value 를 구하는 주제로 여러 자료를 보았습니다.
t 검정의 종류가 다양한 만큼 계산식의 종류와 내용도 복잡하고, 간혹 오류가 있는 자료도 있었습니다.
Wikipedia 기준으로 최종 정리했습니다.
1. T 통계량 수식 정리
t 통계량은 평균의 차이를 불확실성 s/sqrt(n) 으로 표준화한 값입니다.
불확실성은 표본분산을 표본수로 나누어 제곱근을 취해서 구합니다.
표본이 두 개인 경우에는 표본분산과 표본수가 2개씩이므로 각각 표본분산을 표본수로 나눈 값을 더해서 처리합니다.
표본이 두 개인데 분산이 동일한 경우 수식이 아주 아주 복잡해지는데, 표본수가 다른 것을 감안해서 합해주는 개념으로 이해하면 그렇게까지 복잡한 것도 아닙니다.
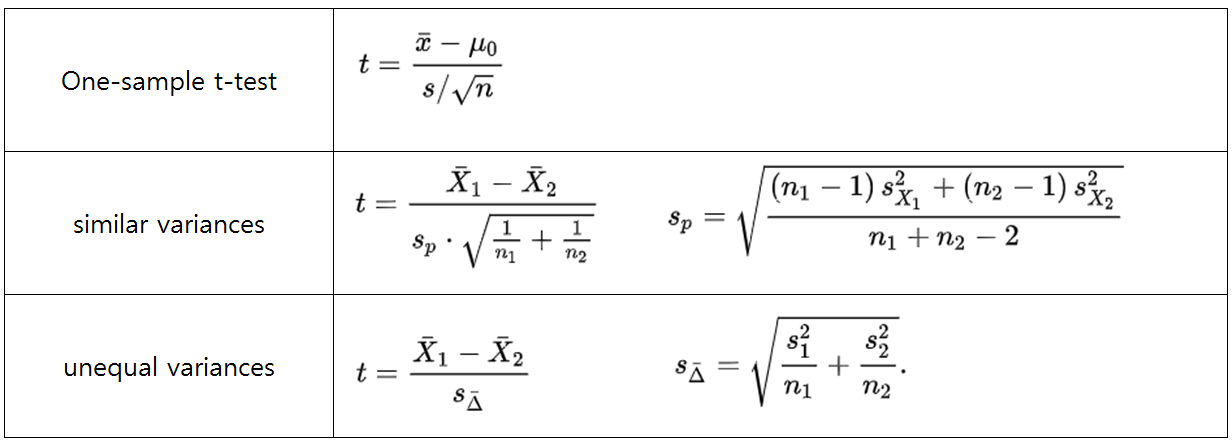
* 이분산의 경우 자유도

2. R 에서 확인
표본수나 정규성 등은 고려하지 않고 t-value 수식 검증만을 목적으로 하는 스크립트입니다.
# 이분산가정 t검정
x <- c(60,54,66,80,72,65,66,67,68)
y <- c(57,50,58,83,70)
var.equal = F
t.test(x, y,
alternative = c("two.sided"),
mu = 0, paired = FALSE, var.equal = var.equal,
conf.level = 0.95,)
mean(x);mean(y)
mean(x) - mean(y)
length(x)
(mean(x) - mean(y)) / sqrt(var(x)/length(x) + var(y)/length(y))

# 등분산가정 t검정
x <- c(60,54,66,80,72,65,66,67,68)
y <- c(57,50,58,83,70)
var.equal = T
t.test(x, y,
alternative = c("two.sided"),
mu = 0, paired = FALSE, var.equal = var.equal,
conf.level = 0.95,)
n1 <- length(x)
n2 <- length(y)
var1 <- var(x)
var2 <- var(y)
MD <- mean(x) - mean(y) # Mean difference
SPN <- (n1 - 1) * var1 + (n2 - 1) * var2 # Numerator of Sp
SPD <- (n1 - 1) + (n2 - 1) # denominator of Sp
MD / (sqrt(SPN / SPD) * sqrt(1/n1 + 1/n2) )

3. 이분산 t검정 d.f.
이분산 가정 t-test의 결과에서 자유도를 보면 df = 5.4037 라고 되어 있습니다.
결과도 정수가 아니라서 보기 불편하지만, 자유도 계산식도 만만치가 않아요
n1 <- length(x)
n2 <- length(y)
var1 <- var(x)
var2 <- var(y)
Num <- (var1/n1+var2/n2)^2
Den <- (var1/n1)^2/(n1-1) + (var2/n2)^2/(n2-1)
Num/Den

Reference
https://en.wikipedia.org/wiki/Student%27s_t-test
https://www.investopedia.com/terms/t/t-test.asp
https://www.jmp.com/ko_kr/statistics-knowledge-portal/t-test/two-sample-t-test.html
https://blog.naver.com/kyoungin90/222081631125
'ADP (R)' 카테고리의 다른 글
| ungroup (0) | 2022.09.03 |
|---|---|
| 부호 검정의 유효 표본수 (0) | 2022.08.29 |
| 쌍체검정 vs 일표본t검정 (0) | 2022.08.27 |
| 오늘의 ADP 준비 / 2022-08-27 토(D29) (0) | 2022.08.27 |
| [Adp 실기 기출 풀이] 25회 혈압약 Paired t-test 문제 (4) | 2022.08.21 |