일표본 중위수 검정을 위해 아래 링크를 공부했습니다.
https://www.statisticshowto.com/symmetric-distribution-2/
https://www.statisticshowto.com/one-sample-median-test/
다음은 위 링크의 내용 중 일부를 해석한 내용이며 정확하지 않을 수 있습니다.
일표본 중위수 검정이란?
일표본 중위수 검정은 가설로 설정한 중위수와 실제 표본의 중위수 사이에 유의미한 차이가 있는지 없는지를 확인하는 검정입니다.
일표본 중위수 검정에는 윌콕슨 부호 순위 검정(Wicloxon Signed Rank Test)과 부호검정(the Sign Test) 두 가지가 있습니다.
검정 방법의 선택
부호검정은 훌륭한 비모수 검정이며 어떠한 가정도 거의 필요로 하지 않지만, 검정력이 제한적이라는 단점이 있습니다.
대칭적인 분포이고 관측치들의 서열을 매길 수 있다면, 좀 더 강한 검정력을 갖고 있는 윌콕슨 부호 순위 검정이 사용될 수 있습니다.
대칭적 분포란?
대칭적 분포는 왼쪽이 오른쪽의 거울과 같은 유형의 분포입니다.
정규분포는 전형적인 대칭적 분포이지만, 대칭적 분포가 반드시 단봉형태일 필요는 없습니다.
쌍봉 또는 다중봉우리 형태의 분포도 가능합니다.
The following bimodal distribution is symmetric, as the two halves are mirror images of each other.
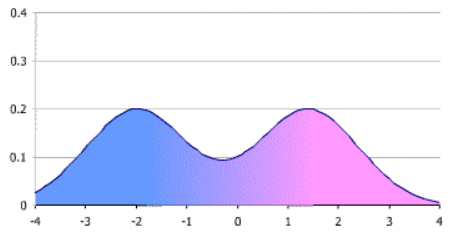
출처 : https://www.statisticshowto.com/symmetric-distribution-2/
부호검정의 다른 특성
부호 검정은 표본수가 매우 작아야 한다거나 위치모수와 같은 데이터가 있는 경우에는 표본의 크기에서 제외시켜야 한다는 자료가 있습니다.
부호검정은 차이(양수 또는 음수)의 방향에 근거한 것만을 제외하고는 윌콕슨 부호-순위 검정과 같다. 변화의 크기는 전적으로 무시한다(순위가 차이의 상대적인 크기를 말해주는 윌콕슨 검정과는 다름.)
이러한 이유로 부호 검정은 표본 수가 매우 작지 않다면(6 이하) 검정력이 부족하다.
출처 : https://blog.naver.com/pmw9440/221934756608
① 부호검정에서 분포에 대한 가정은 단지 데이터들이 연속분포로부터 독립적으로 얻어진 확률표본이다.
② 데이터들 중에 위치모수 θ와 같은 데이터가 있는 경우 검정하기 전에 표본의 크기에서 제외시킨다.
③ 대표본 근사에서 다음과 같은 연속성 수정(continuity correction)을 함으로써 보다 정확한 검정 통계량을 얻을 수 있다.
출처 : https://blog.naver.com/pmw9440/221934756608
'ADP (R)' 카테고리의 다른 글
| ADP 실기 후기 모음 (15,17, 18, 19, 20, 21, 22, 23, 24, 25,26회) (0) | 2022.08.19 |
|---|---|
| [Adp 실기 기출 풀이] 25회 최적투자안 (0) | 2022.08.18 |
| [Adp 실기 기출 풀이] 23회 진공관 수명 (0) | 2022.08.16 |
| [Adp 실기 기출 풀이] 18회 시계열 정상성 체크 (0) | 2022.08.16 |
| 오늘의 ADP 준비 / 2022-08-16 화(D40) (0) | 2022.08.16 |