지난 5월 21일 25회 ADP 필기를 합격했고, 9월 25일 26회 실기를 준비하고 있습니다.
드디어 내일 시험입니다.
1-1. 시계열 문제 풀이 업데이트 실패
기계2. 시계열 문제(유입관광객) 문제를 끝내 제대로 풀지 못했습니다.
log 변환을 해도 분산이 안정화되지 않습니다.
#[Adp 실기 기출 풀이] 25회 시계열 문제 (풀이중)
library(sarima)
library(dplyr)
# 추세가 있고 분산 증가하며 계절성이 존재하는 데이터 생성
# 3개의 결측치도 강제로 생성
set.seed(5678)
ss <- sim_sarima(252, model=list(sar=0.8,nseasons=12, sigma2=1))
data.frame(r=ss) %>%
mutate(no=row_number()) %>%
mutate(visitors=100000+no*100+round(no*r*10)) %>%
select(no, visitors) %>%
mutate(visitors=ifelse(no %in% c(99,121,245),NA,visitors)) -> x
#EDA
summary(x)
library(tseries)
library(forecast)
x %>%
mutate(visitors = ifelse(is.na(visitors),0,visitors)) %>%
select(visitors) %>%
ts(frequency = 12, start = c(2001,01)) %>%
#monthplot(choice = "seasonal", cex.axis = 0.8)
autoplot()
# 결측치 처리
x %>%
mutate(visitors = ifelse(is.na(visitors),111833,visitors)) %>%
select(visitors) %>%
ts(frequency = 12, start = c(2001,01)) %>%
{x2 <<- .} %>%
autoplot()
# 시간의 흐름에 따라 변동폭이 커짐.
# 안정화를 위해 log변환해도 동일??
# 비정상 시계열로 보이는데 adf.test 는 정상이라고 나오고...
plot(x2)
plot(log(x2))
1-2. nsdiffs() 를 통한 계절 차분
sarima 모델링을 위해 Forecasting: Principles and Practice(https://otexts.com/fppkr/index.html) 를 조금 공부했습니다.
gas 데이터는 추세도 존재하고 분산도 안정화되지 않은 샘플입니다. 또한 계절성도 확인됩니다.
auto.arima(gas) 를 돌리면 ARIMA(2,1,1)(0,1,1)[12] 로 확인이 됩니다.
auto.arima 로 블랙박스처럼 튀어 나온 결과 모델을 acf pacf 를 이용해서 직접 유도 해보고자 시도했습니다.
계절차분이 auto.arima 에서 1로 확인되는데, 계절성 차분은 nsdiffs 를 이용해 가능하다고 합니다.

출처 : https://otexts.com/fppkr/stationarity.html
nsdiffs(gas) 를 통해 계절성 부분의 d 도 1이 적당함을 확인할 수 있었습니다.
그렇지만 pq 인수값을 뽑아내지 못했습니다.
decompose stl diff acf pacf 등을 이용해서 pdq 후보 값을 뽑아낼 수 있을 것 같은데 마무리가 안되네요.
# ARIMA(2,1,1)(0,1,1)[12]
auto.arima(gas)
# 차분1
ndiffs(gas)
# 계절차분 필요수 1 (1차차분 후에도 1로확인됨.로그에 1차 차분해도 확인됨 )
nsdiffs(gas)
nsdiffs(diff(gas))
nsdiffs(diff(log(gas)))
ndiffs(decompose(gas)$seasonal)
plot(decompose(gas)$seasonal)
# 분산 안정화
par(mfrow = c(2, 2))
plot(gas,main="gas");plot(log(gas),main="log(gas)")
#비계절 q 인수확인 2 이후에 0에 수렴했다가 다시 주기적으로 벗어남
nsgas <- gas - decompose(gas)$seasonal
ndiffs(nsgas)
plot(nsgas)
Acf(diff(nsgas))
nsgas <- gas - decompose(gas)$seasona 는 아래 자료를 참고해서 시도해보았습니다.
계절부분을 제거하고 비계절 부분의 pdq 를 확인해보려고 하는데 auto.arima 와 유사한 결과를 찾는데 실패했습니다.

출처 : https://kerpect.tistory.com/161
1-3. log 변환을 통한 분산 안정화
par(mfrow = c(2, 2))
plot(gas,main="gas");plot(log(gas),main="log(gas)")
gas 데이터는 log 변환으로 분산이 안정화 됩니다.
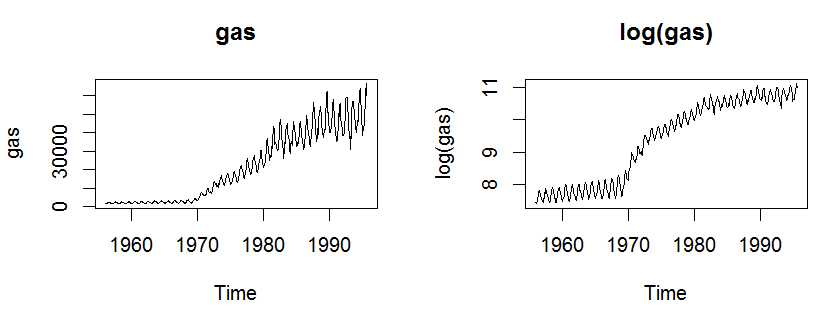
아래 스크립트러 인위적으로 생성한 x 는 log 변환으로 분산이 안정화되지 않습니다.
인위적으로 생성한 방식에 문제가 있는 듯 합니다.
library(sarima)
library(dplyr)
set.seed(5678)
ss <- sim_sarima(252, model=list(sar=0.8,nseasons=12, sigma2=1))
data.frame(r=ss) %>%
mutate(no=row_number()) %>%
mutate(visitors=100000+no*100+round(no*r*10)) %>%
select(no, visitors) %>%
mutate(visitors=ifelse(no %in% c(99,121,245),NA,visitors)) -> x
2. 다항회귀분석 시각화
set.seed(7355826) # Create example data frame
x <- rnorm(200)
y <- rnorm(200) + 0.2 * x^3
data <- data.frame(x, y)
head(data)
my_mod <- lm(y ~ poly(x, 4), # Estimate polynomial regression model
data = data)
summary(my_mod) # Summary statistics of polynomial regression model
plot(y ~ x, data) # Draw Base R plot
lines(sort(data$x), # Draw polynomial regression curve
fitted(my_mod)[order(data$x)],
col = "red",
type = "l")
출처 : https://statisticsglobe.com/add-polynomial-regression-line-plot-r
3. 관리도

출처 : https://www.qimacros.com/free-excel-tips/control-chart-limits/
4. 테미스
테미스는 불균형 데이터를 처리하는 패키지인데 저울을 들고 있는 그리스 신 이름을 따온 것이라고 합니다.
불균형데이터 처리를 위해 공부해볼까 했는데, (제26회)R_package_list.txt 에는 없는 패키지네요.
https://terms.naver.com/entry.naver?docId=3398227&cid=58143&categoryId=58143
테미스는 가이아와 우라노스 사이에서 태어난 티탄 12신 중 하나로, 메티스에 이어 제우스의 두 번째 아내가 된 여신이다.
법, 질서, 정의, 지혜,저울, 칼, 눈을 가린 헝겊
https://www.rdocumentation.org/packages/themis/versions/1.0.0
themis contains extra steps for the recipes package for dealing with unbalanced data.
The name themis is that of the ancient Greek god who is typically depicted with a balance.
5. two sample z-test
모집단의 분산(또는 표준편차)이 알려져있다면 z-test 를 수행하며, 그것은 표본의 크기가 30 보다 크거나 아닌 조건보다 우선인 듯 합니다.

출처: https://vitalflux.com/two-samples-z-test-for-means-formula-examples/
z-test는 두 집단의 평균비교를 통한 가설을 검증하는 분석기법을 말한다. 원칙적으로 모집단의 표준편차를 알고 있는 경우에 z-test를 사용하며, 표준편차를 모를 경우 t-test를 사용한다. 그러나 표본의 크기가 30보다 크다면 ‘중심극한정리(Central Limit Theorem)’에 의해서 정규분포를 따른다고 보고 모집단의 표준편차를 모를지라도 z-test를 사용할 수 있다.
출처 : https://terms.naver.com/entry.naver?docId=20762&cid=43659&categoryId=43659
.
'ADP (R)' 카테고리의 다른 글
| [Adp 실기 기출 풀이] 26회 - 머신러닝 전처리 및 군집분석 (0) | 2022.09.27 |
|---|---|
| ADP 실기 26회 후기(문제 포함) (0) | 2022.09.25 |
| [R] 15분 전력 사용량 요일별 히트맵 샘플 코드 (0) | 2022.09.21 |
| 오늘의 ADP 준비 / 2022-09-20 화(D5) (2) | 2022.09.20 |
| [R] plot las=1 (2) | 2022.09.19 |