5월 21일 제25회 ADP필기 합격 후 첫 번째 실기인 9월 시험을 준비하고 있습니다.
이제 49일밖에 남지 않았네요.
기출 문제들의 형태와 지금까지의 공부 상태를 보면 9월 시험 대비해서 준비가 턱없이 부족한 상황입니다.
시험보기 한달 전에는 EDA 머신러닝 시계열 통계분석 등 유형별로 나만의 코드가 정리 되어 있어야 할 것 같은데 정리는 커녕 유형별 답안 작성도 아직 멀었습니다.
합격후기를 보면 세번 네번의 도전 끝에 간신히 합격을 할까 말까하는 어려운 시험인 듯 합니다.
첫 번째 도전이니 조급해하지 않고 오늘도 할 수 있는 만큼만 공부를 조금 해 봅니다.
TimeSeries 자료 처리가 어렵네요.
이전에 만났던 오류를 오랜만에 해결해보려고 했으나 해결은 못하고 새로운 오류를 만났어요.
첩첩산중이네요.
지난번 문제
Error or Warning message : <simpleError in .common.ts.sanity.check(x): NA in the series>
관련 링크: https://it-freelancer.tistory.com/18
새로운 문제 : Entry “TSDistances” not in registry.
관련 링크 : https://it-freelancer.tistory.com/115
시각화
par mfrow 사용법도 확실히 알았고, graphic 처리시 오류와 조치방법에 대해서도 조금은 더 이해하게 되었어요
figure margins too large .. "여백이 너무 크니 좀 줄여라"라는 에러였네요.'
plot(mpg~wt,data=mtcars)
Error in plot.new() : figure margins too large
par("mar")
par(mar=c(1,1,1,1))
mar 은 margin 의 약자로 보이기도 하지만, mai mar 두 개가 한 세트로 보여 잘 모르겠군요
mai => margin .. inches ?

> plot(lm(mpg~wt,data=mtcars))
Hit <Return> to see next plot:
Hit <Return> to see next plot:
Hit <Return> to see next plot:
Hit <Return> to see next plot:
다음을 눌러가며 그래프를 여러 개 보았었는데, par mfrow 를 이용해서 한번에 표시하는 방법이 있었어요.
par(mfrow = c(2, 2))
plot(lm(mpg~wt,data=mtcars))
회귀의 잔차분석(출처: https://youtu.be/T-5m0ISAHTk?list=LL&t=906 ) 공부하다가 알았어요

시계열분석
지수예측모델 (https://youtu.be/38PuZyCsYUw) 을 공부했어요

시계열이 존재하는 샘플 데이터를 생성해서 시각적으로 확인했어요
library(sarima)
n <- 50
x <- sim_sarima(n, model=list(sar=0.8, nseasons=12, sigma2=1))
t <- ts(x, frequency=12, start=c(1972,4))
# 기본 시각화
par(mfrow=c(1,3))
plot.ts(x)
acf(x,lag=50)
pacf(x,lag=50)

ACF 가 12개월 후에 튀는 것이 계절성분이 있는 자료의 특성이라고 어디서 보았던 것 같은데...
arima 와 지수평활법을 비교해보았어요.
일단은 둘 다 자동으로 나오는 결과로 비교해보았지만, 시험에서는 적절한 시각화 분석을 통해 해당 모델 선정하는 것을 보여줄 수 있도록 좀 더 공부할 예정입니다.
# arima
auto.arima(t)

auto.arima 로 돌려보니 계절성분이 인식되었어요.
결과에 익숙하지 않은 용어와 수치들로 가득합니다.
ARIMA(0,0,0)(0,1,0)[12] with drift
sigma^2 = 0.6149: log likelihood = -44.17
AIC=92.35 AICc=92.69 BIC=95.62
# 지수평활법
ets(t, model="ZZZ")
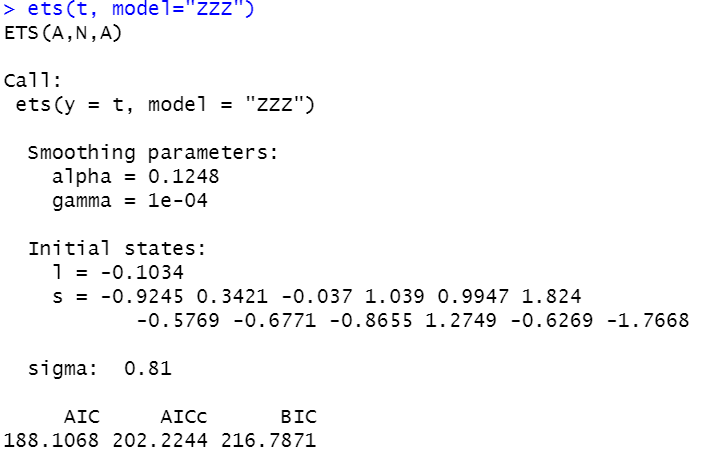
지수평활법을 통해서도 ETS(A,N,A) 즉, 불규칙 추세 계절 성분 중 불규칙 성분과 계절 성분이 인식되었습니다.
AIC 기준으로 92.35 와 188.1068 으로 arima 모델의 성능이 훨씬 우수하네요.
(이렇게 비교하는 것이 맞는지는 아직 모르겠어요)
새로운 데이터 (gas) 를 통해 두 개 방법을 비교해보았어요
auto.arima(gas)
ARIMA(2,1,1)(0,1,1)[12]
sigma^2 = 2587081: log likelihood = -4076.58
AIC=8163.16 AICc=8163.29 BIC=8183.85
ets(gas, model="ZZZ")
불규칙 추세 계절 성분 모두 존재하는 홀트윈터스지수평활법이 적절하며, 가법모델 대신 승법모델로 적합해야합니다.
Ad 에서 d 는 뭔지 공부가 필요하네요
ETS(M,Ad,M)
Call:
ets(y = gas, model = "ZZZ")
Smoothing parameters:
alpha = 0.6946
beta = 0.0272
gamma = 1e-04
phi = 0.98
Initial states:
l = 2023.4144
b = 4.5278
s = 0.8476 0.9197 1.0049 1.0707 1.2084 1.2651
1.176 1.0908 0.9194 0.8921 0.8076 0.7976
sigma: 0.05
AIC AICc BIC
9000.565 9002.062 9075.542
F test
분산분석, aov, anova,var.test,등분산/이분산 구분, levene test, 회귀분석의 가정 중 하나인 등분산성.
모두 다 비슷비슷해 보여 헷갈리고 명확하지 않네요
?var.test 에서 제공하는 샘플 코드입니다.
x <- rnorm(50, mean = 0, sd = 2)
y <- rnorm(30, mean = 1, sd = 1)
var.test(x, y) # Do x and y have the same variance?
var.test(lm(x ~ 1), lm(y ~ 1)) # The same.

자유도 49, 29 인 경우 F통계량 3.9194 에 해당하는 오른쪽 꼬리부분 확률은 9.49e-05 입니다.
대립가설은 "같지 않다" 즉 양측 검증이므로 *2 해주면 0.0001897386 이 나옵니다.
이 값은 위의 var.test 결과의 p-value 입니다.
> pf(3.9194,49,29,lower.tail = F)*2
[1] 0.0001897386
분산분석(aov)은 집단간 평균의 차이가 있는지 확인할 목적의 분산 분석으로서 집단간 분석과 집단내 분석 두 가지의 비율을 봅니다.
회귀분석에 필요한 가정 중 하나인 등분산성은 잔차의 등분산성으로서 독립변수의 변화에 따른 잔차의 분산이 일정해야 한다는 의미입니다.
아래 영상(https://youtu.be/T-5m0ISAHTk?list=LL&t=249)에서 상세히 확인할 수 있습니다.
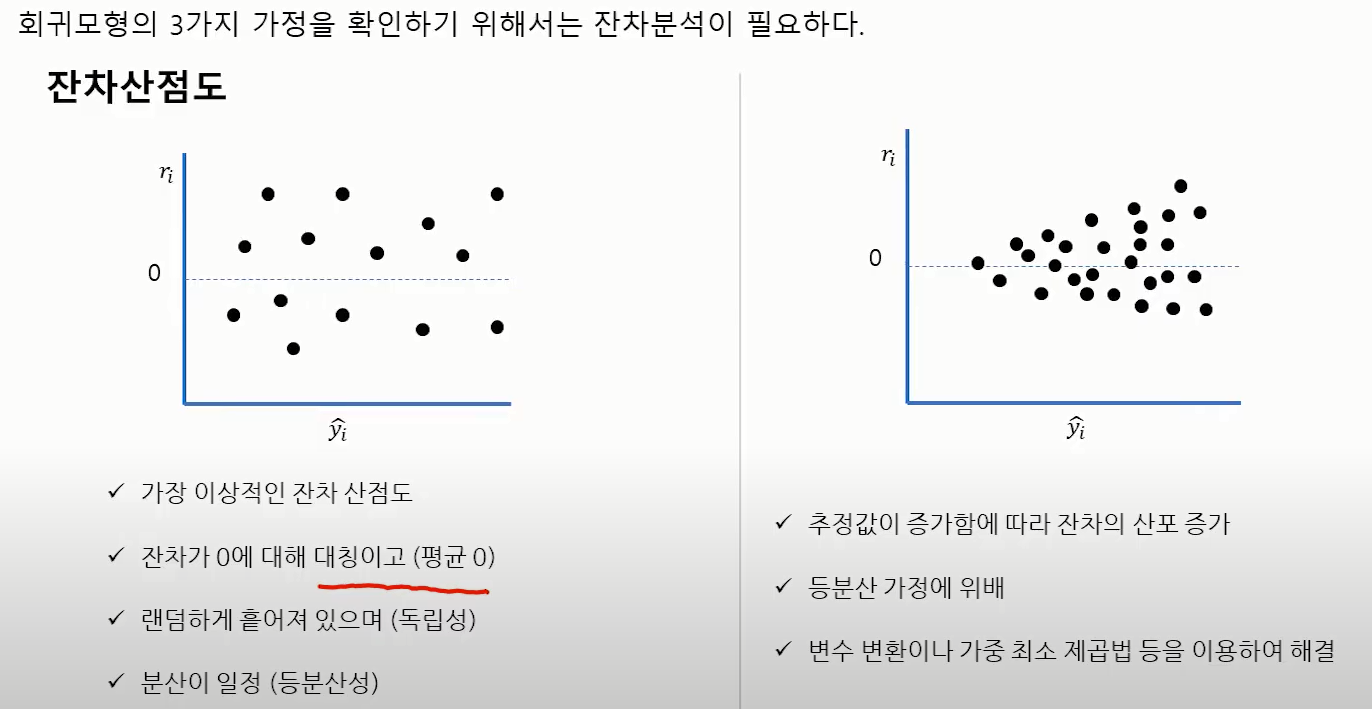
# 잔차
resid(lm(mpg~wt,data=mtcars))
#표준화잔차
rstandard(lm(mpg~wt,data=mtcars))
시계열 정상성의 조건중 하나인 등분산성 테스트에 Goldfeld-Quandt test / Breusch-Pagan test / Bartlett'stest 등을 사용한다고 합니다.
회귀분석 등분산성 확인에는 잔차그림을 통해 시각적으로 확인거나, 수치적인 검정 방법 Breusch-Pagan 검정을 사용합니다.
분산분석의 사후분석시 등분산 여부에 따라 달라지는데 Levene‘s equality of variance test 와 Brown Forsythe 의 동일성 검증을 사용합니다.
t-test 시에 등분산인지 이분산인지에 따라 var.equal 에 TRUE 또는 FALSE 설정을 합니다.
t test 수행 전 두 개 집단이 등분산인지 확인하기 위해서 var.test 를 사용합니다.
[엑셀 통계강의] 24. 독립표본 t검정 (1) F검정( https://youtu.be/-znQjC6lVyI?list=LL&t=75)에서 관련내용 참고하였습니다.

'ADP (R)' 카테고리의 다른 글
| [R] NA in the series 오류 해결 (0) | 2022.08.08 |
|---|---|
| [R] Entry “TSDistances” not in registry 오류 해결 (0) | 2022.08.07 |
| 매개효과분석 (0) | 2022.08.06 |
| 오늘의 ADP 준비 / 2022-08-03 수(D53) (0) | 2022.08.03 |
| 오늘의 ADP 준비 / 2022-08-02 화(D54) (0) | 2022.08.02 |